Copyright © 2015 Powered by MWeb, Theme used GitHub CSS.
数组 \(A\) 是 \([0, 1, ..., N - 1]\) 的一种排列,\(N\) 是数组 \(A\) 的长度。全局倒置指的是 \(i,j\) 满足 \(0 <= i < j < N\) 并且 \([i] > A[j]\) ,局部倒置指的是 \(i\) 满足 \(0 <= i < N\) 并且 \(A[i] > A[i+1]\) 。
当数组 \(A\) 中全局倒置的数量等于局部倒置的数量时,返回 \(true\) 。
示例 1:
输入: \(A = [1,0,2]\)
输出: \(true\)
解释: 有 1 个全局倒置,和 1 个局部倒置。
示例 2:
输入: \(A = [1,2,0]\)
输出: false
解释: 有 2 个全局倒置,和 1 个局部倒置。
注意:
一开始想法比较简单,既然是求逆序对的数量,那么双层for循环一个\(O(n^2)\)的解法就完了。但是第三项注意事项中说了时间限制已经减少,所以毫无意外的超时了。
此时考虑逆序对的性质,全局倒置一定是局部倒置。
对一个\([0,1,...,A.length - 1]\)的排序数组而言,索引\(i\),如果满足\(abs(A[i]-i) <=1\),那么,说明\(i\)只是左移或者右移了一位(或者没变),全局倒置与局部倒置至少同时加一(或者保持不变),仍然满足条件;如果\(abs(A[i] - i) >= 2\),那么,说明\(A[i]\)至少左移或者右移了两位,意味着右边至少有两个比自己小的数(或者左边必然有来2个比自己大且不相邻的数,其中至少一个不相邻)局部(必然<)全局所以造成一定不等,此时不满足条件,直接返回false。
class Solution {
public boolean isIdealPermutation(int[] A) {
if (A.length <3) {
return true;
}
for (int i = 0; i < A.length; i++) {
if (Math.abs(A[i] - i) >= 2) {
return false;
}
}
return true;
}
}
给定两个数组,编写一个函数来计算它们的交集。
示例 1:
输入: nums1 = \([1,2,2,1]\), nums2 = \([2,2]\)
输出: \([2,2]\)
示例 2:
输入: nums1 = \([4,9,5]\), nums2 = \([9,4,9,8,4]\)
输出: [4,9]
说明:
进阶:
问题比较简单。可以遍历两个数组,获得数字出现的频次,然后对比两个频次即可。或者可以直接排序两个数组,然后使用两个指针分别遍历数组即可。
频次法
class Solution {
public int[] intersect(int[] nums1, int[] nums2) {
if(nums1.length > nums2.length) {
return intersect(nums2, nums1);
}
//这里使用hashmap,因为数字是不定长的。
Map<Integer, Integer> map1 = new HashMap<>(nums1.length);
for (Integer i: nums1) {
Integer count = map1.get(i);
if (count == null) {
map1.put(i, 1);
} else {
map1.put(i, count+1);
}
}
Map<Integer, Integer> map2 = new HashMap<>(nums2.length);
for (Integer i: nums2) {
Integer count = map2.get(i);
if (count == null) {
map2.put(i, 1);
} else {
map2.put(i, count+1);
}
}
Iterator iter = map1.entrySet().iterator();
List<Integer> result = new LinkedList();
//遍历两个频次map即可,这里使用小的那个map遍历。可以减少查询次数
while(iter.hasNext()) {
Map.Entry<Integer, Integer> entry = (Map.Entry) iter.next();
Integer key = entry.getKey();
Integer val1 = entry.getValue();
Integer val2 = map2.get(key);
if(val2 != null) {
int count = Math.min(val1, val2);
while (count-- > 0) {
result.add(key);
}
}
}
//最终生成结果,因为没有用从List到int[]的方便转换方法。
int[] res = new int[result.size()];
for(int m=0;m<res.length;m++)
{
res[m]=result.get(m);
}
return res;
}
}
排序遍历法
class Solution {
public int[] intersect(int[] nums1, int[] nums2) {
if(nums1.length > nums2.length) {
return intersect(nums2, nums1);
}
List<Integer> result = new LinkedList();
//排序两个数组
Arrays.sort(nums1);
Arrays.sort(nums2);
//遍历两个数组
for (int i = 0,j=0; i<nums1.length && j<nums2.length;) {
//相等则加入result
if (nums1[i] == nums2[j]) {
result.add(nums1[i]);
i++;
j++;
} else if (nums1[i] < nums2[j]){
// 这里注意只有其中一个往前推进。
i++;
} else {
j++;
}
}
int[] res = new int[result.size()];
for(int m=0;m<res.length;m++)
{
res[m]=result.get(m);
}
return res;
}
}
给定仅有小写字母组成的字符串数组 A,返回列表中的每个字符串中都显示的全部字符(包括重复字符)组成的列表。例如,如果一个字符在每个字符串中出现 3 次,但不是 4 次,则需要在最终答案中包含该字符 3 次。
你可以按任意顺序返回答案。
示例 1:
输入:\(["bella","label","roller"]\)
输出:\(["e","l","l"]\)
示例 2:
输入:\(["cool","lock","cook"]\)
输出:\(["c","o"]\)
提示:
首先需要将每一个字符串进行字母的数量统计。然后遍历数量数组,获取每个字符的最小出现次数,即为答案。
数量统计有多种做法,二维数组、hashmap。此题中使用了二维数组。
class Solution {
public List<String> commonChars(String[] A) {
//生成一个二维数组用于保存词频
int[][] array = new int[A.length][26];
//词频统计
for (int i = 0; i < A.length; i++) {
String s = A[i];
for (char c : s.toCharArray()) {
array[i][c - 97]++;
}
}
List<String> result = new LinkedList<>();
for (int i = 0; i < 26; i++) {
if(array[0][i]==0) {
continue;
}
//得到第一组词频
int count = array[0][i];
for (int j = 1; j < A.length; j++) {
if (array[j][i] == 0){
count = 0;
break;
}
count = Math.min(count, array[j][i]);
}
//如果词频大于0,那么加入结果中
if (count > 0) {
char c = (char) (97 + i);
String s = Character.toString(c);
while (count-- >0) {
result.add(s);
}
}
}
return result;
}
}
给定一个二进制数组, 计算其中最大连续1的个数。
示例 1:
输入: \([1,1,0,1,1,1]\)
输出: \(3\)
解释: 开头的两位和最后的三位都是连续\(1\),所以最大连续\(1\)的个数是 \(3\).
注意:
此题比较简单,一次遍历即可完成。直接上代码。
class Solution {
public int findMaxConsecutiveOnes(int[] nums) {
int result = 0;
int curr = 0;
for(int i: nums) {
if (i == 0) {
curr = 0;
} else{
curr++;
result = Math.max(result, curr);
}
}
return result;
}
}
最大树定义:一个树,其中每个节点的值都大于其子树中的任何其他值。
给出最大树的根节点 \(root\)。
就像之前的问题那样,给定的树是从表 \(A(root = Construct(A))\)递归地使用下述 \(Construct(A)\) 例程构造的:
假设 \(B\) 是 \(A\) 的副本,并附加值 \(val\)。保证 \(B\) 中的值是不同的。
返回 \(Construct(B)\)。
示例 1:

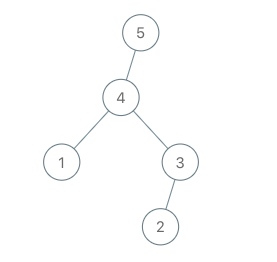
输入: \(root = [4,1,3,null,null,2], val = 5\)
输出: \([5,4,null,1,3,null,null,2]\)
解释: \(A = [1,4,2,3], B = [1,4,2,3,5]\)
示例 2:


输入:\(root = [5,2,4,null,1], val = 3\)
输出:\([5,2,4,null,1,null,3]\)
解释:\(A = [2,1,5,4], B = [2,1,5,4,3]\)
示例 3:


输入:\(root = [5,2,3,null,1], val = 4\)
输出:\([5,2,4,null,1,3]\)
解释:\(A = [2,1,5,3], B = [2,1,5,3,4]\)
这道题本身不难,难得是理解题意,一开始我还在想示例2中的3放在5前面似乎也并无不可。后来才发现,其实\(val\)是追加在\(A\)末尾的,而不是随便放在哪个位置的。既然这样,考虑一下\(val\)与\(root\)的大小关系,一共有三种情况:
递归完成后返回root即可。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode insertIntoMaxTree(TreeNode root, int val) {
// 情况1
if (root == null) {
return new TreeNode(val);
}
// 情况2
if (root.val < val) {
TreeNode node = new TreeNode(val);
node.left = root;
return node;
}
// 情况3
root.right = insertIntoMaxTree(root.right,val);
//最终递归返回
return root;
}
}
给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下:
Example 1:
输入: \([3,2,1,6,0,5]\)
输入: 返回下面这棵树的根节点:
6
/ \
3 5
\ /
2 0
\
1
注意:
通过定义,我们发现,可以通过遍历获取到此次遍历的根结点,然后再次分别遍历根节点左边的子数组获取此次遍历的根节点的左儿子,遍历根节点右边的子数组获取根节点的右儿子。需要注意的点是儿子是否存在有两种情况,需要在遍历子数组的时候处理好。
整体没有太大难度,边界条件处理好即可。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode constructMaximumBinaryTree(int[] nums) {
return treefy(nums, 0, nums.length-1);
}
private TreeNode treefy(int[] nums, int start, int end){
//当start==end时,表示为叶节点了,可以生成叶节点跳出了
if(start == end) {
return new TreeNode(nums[start]);
}
//当start>end时,表示叶节点为空,返回null
if (start>end) {
return null;
}
//遍历start与end之间的元素,找到最大值,生成节点。
int maxIndex = start;
for(int i = start; i <= end; i++) {
if (nums[i] > nums[maxIndex]) {
maxIndex = i;
}
}
//找到最大值后,递归调用左儿子与右儿子
TreeNode node = new TreeNode(nums[maxIndex]);
node.left = treefy(nums, start, maxIndex - 1);
node.right = treefy(nums,maxIndex + 1, end);
return node;
}
}
Copyright © 2015 Powered by MWeb, Theme used GitHub CSS.