Copyright © 2015 Powered by MWeb, Theme used GitHub CSS.
给定一个二叉树,它的每个结点都存放一个 0-9 的数字,每条从根到叶子节点的路径都代表一个数字。
例如,从根到叶子节点路径 \(1->2->3\) 代表数字 \(123\)。
计算从根到叶子节点生成的所有数字之和。
说明: 叶子节点是指没有子节点的节点。
示例 1:
输入: \([1,2,3]\)
1
/ \
2 3
输出: 25
解释:
从根到叶子节点路径 \(1->2\) 代表数字 \(12\).
从根到叶子节点路径 \(1->3\) 代表数字 \(13\).
因此,数字总和 = \(12 + 13 = 25\).
示例 2:
输入:\([4,9,0,5,1]\)
4
/ \
9 0
/ \
5 1
输出: \(1026\)
解释:
从根到叶子节点路径 \(4->9->5\) 代表数字 \(495\).
从根到叶子节点路径 \(4->9->1\) 代表数字 \(491\).
从根到叶子节点路径 \(4->0\) 代表数字 \(40\).
因此,数字总和 = \(495 + 491 + 40 = 1026\).
整体难度不大,使用深度优先搜索算法递归即可
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private int result = 0;
public int sumNumbers(TreeNode root) {
dfs(root,0);
return result;
}
private void dfs(TreeNode root, int curr) {
if (root == null) {
return;
}
//需要注意的是这里要乘10再加。
curr = curr *10 + root.val;
if(root.left ==null && root.right == null) {
result += curr;
return;
}
//递归左子树
bfs(root.left, curr);
//递归右子树
bfs(root.right,curr);
}
}
翻转一棵二叉树。
示例:
输入:
4
/ \
2 7
/ \ / \
1 3 6 9
输出:
4
/ \
7 2
/ \ / \
9 6 3 1
很简单的递归调用即可。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root ==null) {
return root;
}
invert(root);
return root;
}
private void invert(TreeNode root) {
if (root ==null) {
return;
}
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
invert(root.left);
invert(root.right);
}
}
这道题是HomeBrew的作者 Max Howell 的一条推特中的题。
给定一个二叉树,返回它的中序 遍历。
示例:
输入: \([1,null,2,3]\)
1
\
2
/
3
输出: \([1,3,2]\)
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
经典的算法题,没什么可说的。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
mid(root, result);
return result;
}
private void mid(TreeNode root, List<Integer> result) {
if (root ==null) {
return;
}
//先递归左子树
mid(root.left,result);
//递归完成后加入本节点
result.add(root.val);
//再递归右子树
mid(root.right, result);
}
}
构建一个栈,只要有左子树就一直压栈,直到左子树为空,出栈后将结果加入到result,然后将当前指针指向当前节点的右子树,进行下一轮压栈处理。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> stack = new Stack<>();
while (root != null || !stack.empty()) {
//左子树一直压栈
while(root != null) {
stack.push(root);
root = root.left;
}
//出栈
root = stack.pop();
result.add(root.val);
//切换到右子树进行下一轮
root = root.right;
}
return result;
}
}
给定一个二叉树,返回它的 前序 遍历。
示例:
输入: \([1,null,2,3]\)
1
\
2
/
3
输出: \([1,2,3]\)
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
没什么可说的。直接上代码吧。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private List<Integer> result = new LinkedList<>();
public List<Integer> preorderTraversal(TreeNode root) {
if (root == null) {
return result;
}
preorder(root);
return result;
}
public void preorder(TreeNode root) {
if (root == null) {
return;
}
//先将root.val加入result
result.add(root.val);
//递归左子树
preorder(root.left);
//递归右子树
preorder(root.right);
}
}
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private List<Integer> result = new LinkedList<>();
public List<Integer> preorderTraversal(TreeNode root) {
if (root == null) {
return result;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
result.add(node.val);
//需要注意这里right要先压栈 其他的基本无压力。
if (node.right !=null) {
stack.push(node.right);
}
if (node.left !=null) {
stack.push(node.left);
}
}
return result;
}
}
最大树定义:一个树,其中每个节点的值都大于其子树中的任何其他值。
给出最大树的根节点 \(root\)。
就像之前的问题那样,给定的树是从表 \(A(root = Construct(A))\)递归地使用下述 \(Construct(A)\) 例程构造的:
假设 \(B\) 是 \(A\) 的副本,并附加值 \(val\)。保证 \(B\) 中的值是不同的。
返回 \(Construct(B)\)。
示例 1:

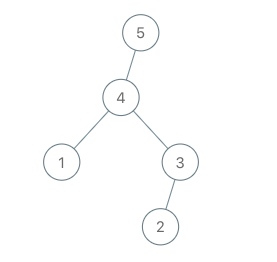
输入: \(root = [4,1,3,null,null,2], val = 5\)
输出: \([5,4,null,1,3,null,null,2]\)
解释: \(A = [1,4,2,3], B = [1,4,2,3,5]\)
示例 2:


输入:\(root = [5,2,4,null,1], val = 3\)
输出:\([5,2,4,null,1,null,3]\)
解释:\(A = [2,1,5,4], B = [2,1,5,4,3]\)
示例 3:


输入:\(root = [5,2,3,null,1], val = 4\)
输出:\([5,2,4,null,1,3]\)
解释:\(A = [2,1,5,3], B = [2,1,5,3,4]\)
这道题本身不难,难得是理解题意,一开始我还在想示例2中的3放在5前面似乎也并无不可。后来才发现,其实\(val\)是追加在\(A\)末尾的,而不是随便放在哪个位置的。既然这样,考虑一下\(val\)与\(root\)的大小关系,一共有三种情况:
递归完成后返回root即可。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode insertIntoMaxTree(TreeNode root, int val) {
// 情况1
if (root == null) {
return new TreeNode(val);
}
// 情况2
if (root.val < val) {
TreeNode node = new TreeNode(val);
node.left = root;
return node;
}
// 情况3
root.right = insertIntoMaxTree(root.right,val);
//最终递归返回
return root;
}
}
给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下:
Example 1:
输入: \([3,2,1,6,0,5]\)
输入: 返回下面这棵树的根节点:
6
/ \
3 5
\ /
2 0
\
1
注意:
通过定义,我们发现,可以通过遍历获取到此次遍历的根结点,然后再次分别遍历根节点左边的子数组获取此次遍历的根节点的左儿子,遍历根节点右边的子数组获取根节点的右儿子。需要注意的点是儿子是否存在有两种情况,需要在遍历子数组的时候处理好。
整体没有太大难度,边界条件处理好即可。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode constructMaximumBinaryTree(int[] nums) {
return treefy(nums, 0, nums.length-1);
}
private TreeNode treefy(int[] nums, int start, int end){
//当start==end时,表示为叶节点了,可以生成叶节点跳出了
if(start == end) {
return new TreeNode(nums[start]);
}
//当start>end时,表示叶节点为空,返回null
if (start>end) {
return null;
}
//遍历start与end之间的元素,找到最大值,生成节点。
int maxIndex = start;
for(int i = start; i <= end; i++) {
if (nums[i] > nums[maxIndex]) {
maxIndex = i;
}
}
//找到最大值后,递归调用左儿子与右儿子
TreeNode node = new TreeNode(nums[maxIndex]);
node.left = treefy(nums, start, maxIndex - 1);
node.right = treefy(nums,maxIndex + 1, end);
return node;
}
}
给定一个二叉树,返回它的 后序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [3,2,1]
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
递归方法很简单,不再赘述。迭代方法一般考虑用双栈法。java的LinkedList提供了add(0,value)的方法,可以直接使用这个作为第二个栈与返回值。
递归
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private List<Integer> result = new LinkedList<>();
public List<Integer> postorderTraversal(TreeNode root) {
if (root == null) {
return result;
}
dfs(root);
return result;
}
private void dfs(TreeNode root) {
if (root == null) {
return;
}
dfs(root.left);
dfs(root.right);
result.add(root.val);
}
}
迭代
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private List<Integer> result = new LinkedList<>();
public List<Integer> postorderTraversal(TreeNode root) {
if (root == null) {
return result;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while(!stack.empty()) {
TreeNode node = stack.pop();
//直接add(0,val);
result.add(0, node.val);
//注意这里是左先入栈
if (node.left !=null){
stack.push(node.left);
}
//然后是右入栈
if(node.right !=null) {
stack.push(node.right);
}
}
return result;
}
}
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
示例 1:
给定二叉树\([3,9,20,null,null,15,7]\)
3
/ \
9 20
/ \
15 7
返回\(true\)
示例 2:
给定二叉树 \([1,2,2,3,3,null,null,4,4]\)
1
/ \
2 2
/ \
3 3
/ \
4 4
返回\(false\)
深度优先搜索,首先获取左右子树的深度,判断相差是否小于1,然后递归左右子树即可,需要注意的一点是获取左右子树深度的时候需要+1
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean isBalanced(TreeNode root) {
if(root == null) {
return true;
}
//获取左子树的深度
int left = dfs(root.left);
//获取右子树的深度
int right = dfs(root.right);
//判断左右子树深度差 递归调用左右子树。
return Math.abs(left-right) <=1 && isBalanced(root.left) && isBalanced(root.right);
}
//获取树的深度
private int dfs(TreeNode root) {
if(root == null) {
return 0;
}
int left = dfs(root.left);
int right = dfs(root.right);
//左右深度+1的最大值。
return Math.max(left, right) + 1;
}
}
给定一个二叉树,找到最长的路径,这个路径中的每个节点具有相同值。 这条路径可以经过也可以不经过根节点。
**注意:**两个节点之间的路径长度由它们之间的边数表示。
示例 1:
输入:
5
/ \
4 5
/ \ \
1 1 5
输出 \(2\)
示例 2:
输入:
1
/ \
4 5
/ \ \
4 4 5
输出: \(2\)
注意: 给定的二叉树不超过\(10000\)个结点。 树的高度不超过\(1000\)。
基本想法就是深度优先遍历。遍历时,判断左右儿子的值与自己的值是否相等,相等则result++,否则置为0即可。没有什么难度。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private int result = 0;
public int longestUnivaluePath(TreeNode root) {
if (root != null) {
dfs(root);
}
return result;
}
private int dfs(TreeNode root) {
if (root ==null) {
return 0;
}
//计算左子树的同值路径
int left = dfs(root.left);
//判断左儿子与自己的值是否相等,相等则++ 否则置为0
if (root.left == null || root.val !=root.left.val) {
left = 0;
} else {
left ++;
}
//计算右子树的同值路径
int right = dfs(root.right);
//同左儿子的判断
if (root.right == null || root.val !=root.right.val) {
right = 0;
} else {
right ++;
}
//需要注意的是这里的max为left+right与result的判断。
result = Math.max(left + right,result);
return Math.max(left, right);
}
}
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过根结点。
示例 :
给定二叉树
digraph G {
{
node [margin=0 width=0.1 shape=circle style=filled]
1 -> 2 [arrowhead=none]
1 -> 3 [arrowhead=none]
2 -> 4 [arrowhead=none]
2 -> 5 [arrowhead=none]
}
}
返回\(3\),它的长度是路径 \([4,2,1,3]\) 或者 \([5,2,1,3]\)。
**注意:**两结点之间的路径长度是以它们之间边的数目表示。
此题是二叉树深度搜索的扩展,考虑设置一个全局变量result,每次递归时判断一次左子树深度+右子树深度 是否大于result,如果大于,那么将result替换成和,递归完成时,返回result即可。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private int result = 0;
public int diameterOfBinaryTree(TreeNode root) {
// 深度优先遍历+判断一次result大小即可。
dfs(root);
return result;
}
private int dfs(TreeNode root) {
if (root == null) {
return 0;
}
//递归左子树
int right = dfs(root.right);
//递归右子树
int left = dfs(root.left);
//左子树深度+右子树深度就是走过当前节点的直径长度
if (left + right > result) {
result = left + right;
}
//返回当前节点深度+1.递归到上一层参与计算
return Math.max(left, right) + 1;
}
}
Copyright © 2015 Powered by MWeb, Theme used GitHub CSS.