问题

假设你正在爬楼梯。需要 \(n\) 阶你才能到达楼顶。

每次你可以爬 \(1\) 或 \(2\) 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 \(n\) 是一个正整数。

示例 1：

输入： \(2\)
输出： \(2\)
解释： 有两种方法可以爬到楼顶。

1. \(1\) 阶 + \(1\) 阶
2. \(2\) 阶

示例 2：

输入： \(3\)
输出： \(3\)
解释： 有三种方法可以爬到楼顶。

1. \(1\) 阶 + \(1\) 阶 + \(1\) 阶
2. \(1\) 阶 + \(2\) 阶
3. \(2\) 阶 + \(1\) 阶

解答1

此题目可以说是最经典（另一种说法是最“容易”）的动态规划的题目。
动态规划是将一个大问题分解为多个简单的子问题来求解的方法。
动态规划常常适用于有重叠子问题与最优子结构的问题。

思路

1. 设\(f(n)\)为总的方法数量
2. 可以看到，到第\(n\)阶的方法其实一共有两种方式
   • 从第\(n-1\)阶爬一步到达第\(n\)阶
   • 从第\(n-2\)阶爬两步到达第\(n\)阶
3. 因此可以总结出公式
   \(f(n) = \begin{cases} 1, & \text{\)n = 1\(} \\ 2,& \text{\)n = 2\(} \\ f(n-1) +f(n-2), & \text{\)n>2\(} \end{cases}\)可以发现，这个就是斐波那契数列的变种。

##代码1

java实现

class Solution {
    public int climbStairs(int n) {
        return resolve(n);
    }
    public int resolve(int n) {
        if (n==1) {
            return 1;
        }
        if (n==2) {
            return 2;
        }
        return resolve(n-1)+resolve(n-2);
    }
}

代码非常的简洁，马上丢到leetcode上跑一次，居然执行了10801 ms。击败了0.98%的人。。。

解法2

解法1虽然勉强能跑，但是有一个非常严重的问题是，重复计算量过大。
\(f(n)与f(n-1)均用到了f(n-2)\)但是因为并没有暂存的地方，导致\(f(n-2)\)被计算了两次。
比如计算\(f(5)\)：

    
    strict graph { 
      a -- b
      a -- b
      b -- a [color=blue]
    } 
    ```
此时考虑到以往的数据会被重复使用，那么何不做一个数组暂存数据呢。
## 代码2
### java实现
```java
class Solution {
    public int climbStairs(int n) {
        int[] cache = new int[n+1];
        return resolve(n);
    }
    public int resolve(int n, int[] cache) {
        if (n==1) {
            return 1;
        }
        if (n==2) {
            return 2;
        }
        if (cache[n] ==0) {
            cache[n] = resolve(n-1,cache) +resolve(n-2,cache);
        }
        return cache[n];
    }
}

此方法4ms执行完成。

解法3

上述两种方法，均是递归调用，如何转为迭代呢？

代码3

java实现

class Solution {
    public int climbStairs(int n) {
        int[] cache = new int[n+1];
        cache[0] = cache[1] = 1;
        for(int i=2;i<=n;i++) {
            cache[i] = cache[i-1] + cache[i-2];
        }
        return cache(n);
    }
}

问题

给定一个包含非负数的数组和一个目标整数 \(k\)，编写一个函数来判断该数组是否含有连续的子数组，其大小至少为 \(2\)，总和为 \(k\) 的倍数，即总和为 \(n*k\)，其中 \(n\) 也是一个整数。

示例 1:

输入: \([23,2,4,6,7], k = 6\)
输出: True
解释: \([2,4]\) 是一个大小为 \(2\) 的子数组，并且和为 \(6\)。

示例 2:

输入: \([23,2,6,4,7], k = 6\)
输出: True
解释: \([23,2,6,4,7]\)是大小为 \(5\) 的子数组，并且和为 \(42\)。

说明:

数组的长度不会超过10,000。
你可以认为所有数字总和在 32 位有符号整数范围内。

解答1

遍历不同长度的子数组，判断是不是能被整除即可。有一个优化点在于可以用动态规划的思路。在len+1长度的子数组遍历时，可以用到len长度的子数组已经计算好的值，不需要再次计算了。

需要clone一份nums数据，空间复杂度是\(O(n)\)

源码1

java实现

class Solution {
    public boolean checkSubarraySum(int[] nums, int k) {
        //新增一个数组保存上一轮的全部sum数据
        //这里容易出错的地方在于将sums的数据初始化为0。会造成基础数据就不对。
        int[] sums = nums.clone();
        //从len=2开始，进行长度不同的遍历
        for(int len=2;len<=nums.length;len++) {
            for(int i = 0; i<=nums.length-len; i++) {
                //此时将sums[i]的数据与nums[i+len-1]的数据相加获得新值
                sums[i] += nums[i+len-1];
                //排除掉[0,0],0 的特殊情况
                if(sums[i] ==0) {
                    return true;
                }
                //判断当前值是不是可以整除，可以直接返回true
                if (k!=0&& sums[i]%k==0) {
                    return true;
                }
            }
        }       
        //默认情况
        return false;
    }
}

解答2

引入一个概念，前缀和（prefix sum）。

给定一个数组\(x\)，数组元素为\(x_0,x_1,x_2,...x_{n-1},x_n\)
如果有数组\(y\),满足如下条件
\(y_0=x_0\)
\(y_1=x_0+x_1\)
\(y_2=x_0+x_1+x_2\)
\(...\)
\(y_{n-1}=x_0+x_1+x_2+...+x_{n-1}\)
\(y_n=x_0+x_1+x_2+...+x_{n-1}+x_{n}\)
那么称\(y\)为\(x\)的前缀和数组
例子

此时可以发现，数组\(x\)的子序列和均可由前缀和数组\(y\)获得，如\({x_a}\)至\({x_b}\)子序列的和，可以由\(y_b-y_{a-1}\)得到。而且也可以用到动态规划的思路，一次遍历生成\(y\)数组，然后接下来的遍历就可以复用\(y\)数组了。

源码2

java实现

class Solution {
    public boolean checkSubarraySum(int[] nums, int k) {
        //生成前缀和数组，此时已经可以判断一次了
        int[] presums = new int[nums.length];
        for(int i=0;i<nums.length;i++) {
            if (i==0) {
                presums[0]=nums[0];
            } else {
                presums[i] = presums[i-1] + nums[i];
                if (presums[i] == 0) {
                    return true;
                }
                if (k!=0 && presums[i]%k==0) {
                    return true;
                }
            }
        }
        //此时遍历连续子数组的和
        for (int i=1;i<presums.length;i++) {
            for(int len=2;len<=i;len++) {
                //这一步是获取从i-len+1到i的子数组的和
                int sub = presums[i]-presums[i-len];
                if(sub ==0) {
                    return true;
                }
                if (k!=0 && sub%k==0) {
                    return true;
                }
            }
        }
        //默认情况
        return false;
    }
}

代码整体没有难度，需要关注的点在于遍历子数组的和时的边界问题，因为题目要求是最少长度为2，所以len这里需要赋值为2，len<=i的原因在于需要将presums[0]首位数扣除。

解法3

仍然需要解法2的前缀和的概念。
假设有两个索引值\(a与b,y_a = m*k + mod_a,y_b = n*k + mod_b\)其中\(mod_a与mod_b\)为\(y_a与y_b整除k的余数\)。不难发现这么一个情况，如果\(mod_a==mod_b并且 b-a>1\)，那么\(a\)到\(b\)的子数组和就是满足要求的数组。
此时可以考虑，将每一个\(mod\)与其索引值放入一个map中，key为\(mod\),value为索引值。每次循环时，判断新值的\(mod\)是否保存在map中，如果存在，那么判断两个索引值之间的差值是否大于1，大于1就返回true即可
有一种特殊情况，就是\(nums_0==0\)并且\(nums_i\%k==0\)，为了处理这种情况，设置键值对(0,-1)
需要处理连续两个0以及k=0的特殊情况

源码3

class Solution {
    public boolean checkSubarraySum(int[] nums, int k) {
        //先处理特殊情况
        //当nums的长度小于2时，必然false
        if (nums.length<2) return false;
        //当相邻两个值均为0时，必然true
        for(int i=0;i<nums.length-1;i++) {
            if(nums[i]==0&&nums[i+1]==0) return true;
        }
        //此时排除掉上一种情况时，如果k==0，那么必然为false
        if (k==0) return false;
        //开始循环
        //构造一个map放入mod与索引
            Map<Integer,Integer> map = new HashMap<>();
        //写入特殊情况的键值对(0,-1)
        map.put(0,-1);
        //构造一个全局变量供每次循环累加使用
        int sum=0;
        for(int i=0;i<nums.length;i++) {
            sum +=nums[i];
            //取余
            int mod = sum%k;
            //判断map中是否已经包含了mod值，
            if (map.containsKey(mod)) {
                //当两个索引值相减大于1时，说明有2个元素及以上的子数组满足条件
                if (i-map.get(i) > 1) {
                    return true;
                }
            } else {
                //将键值对放入map中
                map.put(mod, i);
            }
        }
        //默认情况
        return false;
    }
}

总结

此题目的解法众多，但是快速找到一个时间复杂度与空间复杂度均低的解法还是需要一些思考的。解法1与解法2在leetcode中的耗时大概在66ms左右，解法3耗时在13ms左右。

问题

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

你可以假设数组中无重复元素。

示例 1:

输入: [1,3,5,6], 5
输出: 2

示例 2:

输入: [1,3,5,6], 2
输出: 1

示例 3:

输入: [1,3,5,6], 7
输出: 4

示例 4:

输入: [1,3,5,6], 0
输出: 0

解答

此题没有难度，遍历数组，分为两种情况

• 数组当前值nums[i]大于等于target，此时，直接返回i即可，因为不管是大于还是等于，target的位置都是在i处
• 遍历后仍然没有返回，此时说明target大于全部的nums中的数据，此时返回nums.length

代码

java实现

class Solution {
    public int searchInsert(int[] nums, int target) {
        for(int i=0;i<nums.length;i++) {
            //第一种情况
            if (nums[i]>=target) {
                return i;
            }
        }
        //第二种情况
        return nums.length;
    }
}

问题

给定一个未排序的数组，判断这个数组中是否存在长度为 3 的递增子序列。

数学表达式如下:

如果存在这样的 i, j, k, 且满足 0 ≤ i < j < k ≤ n-1，
使得 arr[i] < arr[j] < arr[k] ，返回 true ; 否则返回 false 。
说明: 要求算法的时间复杂度为 O(n)，空间复杂度为 O(1) 。

示例 1:

输入: [1,2,3,4,5]
输出: true

示例 2:

输入: [5,4,3,2,1]
输出: false

解答

1. 使用两个int变量m1与m2，初始化为整型最大值。
2. 开始遍历数组,此时分三种情况
   • m1大于等于数组当前值nums[i]，此时，将数组当前值nums[i]赋值给m1
   • m1小于数组当前值nums[i]、m2大于数组当前值nums[i]，此时，将数组当前值赋值给m2。这里有个隐含的状态是，m2更新代表着我们已经找到了一个递增的二元子序列。接下来的查找中只需要找到一个值大于m2就说明存在递增的三元子序列，直接返回true即可。
   • m2也小于数组当前值nums[i]，因为前两种情况进入时已经找到了递增的二元子序列，此时直接返回true即可。
3. 当在遍历中没有返回时，代表数组中最多只有递增的二元子序列，直接返回false即可

注意在循环中，实际上每次判断都会尽量减小m1与m2的值，毕竟m2的值越小，在接下来的数据中大于m2的可能性就更高

代码

java实现

class Solution {
    public boolean increasingTriplet(int[] nums) {
        //两个变量。初始化为整型最大值。
        int m1 = Integer.MAX_VALUE;
        int m2 = Integer.MAX_VALUE;
        for(int i = 0; i < nums.length; i++) {
            //上述的第一种情况
            if (m1>=nums[i]) {
                m1=nums[i];
            } else {
                //上述的第二种情况
                if (m2>=nums[i]) {
                    m2=nums[i];
                } else {
                    //上述的第三种情况
                    return true;
                }
        }
        //遍历过程中没有返回的情况。
        return false;
    }
}

{"errorCode":0,"errorMessage":"",data:{"name":"kotlin",age:12}}

例子

有一个Controller如下所示

@Controller
class MyController {

    @RequestMapping("user")
    @ResponseBody
    fun getUser(): User {
        return User("kotlin", 12)
    }
}

data class User(val name: String, val age: Int)

该Controller下有一个getUser的接口，返回一个User类，User类有两个属性，name与age。
启动项目后访问http://localhost:8080/user可以得到如下返回值

{
  "name": "kotlin",
  "age": 12
}

普通的实现方式

直接修改这个getUser方法

1. 新定义一个类

   data class Result(val errorCode:Int, val errorMessage:String, val data:Any?)
   

2. 修改getUser接口的返回值

   @RequestMapping("user")
   @ResponseBody
   fun getUser(): Result {
       return Result(0,"",User("kotlin", 12))
   }
   

3. 重启服务并且访问http://localhost:8080/user可以得到如下返回值：

   {
     "errorCode": 0,
     "errorMessage": "",
     "data": {
       "name": "kotlin",
       "age": 12
     }
   }
   

   可以发现这种是实现了文章开头的返回格式的。

但是这种实现方式有一个很严重的问题是，每增加一个接口都需要加上一些格式化代码。这样会造成大量的冗余代码的出现。而且如何以后重构代码时希望去掉这种格式的返回值的话，每一个接口都需要删除掉代码。

使用ResponseBodyAdvice的实现方式

spring4.1中引入了ResponseBodyAdvice接口，继承这个接口可以很容易的实现格式化返回值的需求。

1. 新增一个MyAdvice继承ResponseBodyAdvice

   @ControllerAdvice
   class MyAdvice : ResponseBodyAdvice<Any> {
       //此方法可以过滤需要进行格式化输出的请求，本例中默认全部支持。因此直接返回true
       override fun supports(returnType: MethodParameter, converterType: Class<out HttpMessageConverter<*>>): Boolean {
           return true
       }
       //此方法将Controller中的返回值body，包装成格式化输出的格式，因此直接返回了Result的实例
       override fun beforeBodyWrite(body: Any?,
                                    returnType: MethodParameter,
                                    selectedContentType: MediaType,
                                    selectedConverterType: Class<out HttpMessageConverter<*>>,
                                    request: ServerHttpRequest,
                                    response: ServerHttpResponse): Any? {
           return Result(0, "", body)
       }
   }
   

2. 重启服务并且访问http://localhost:8080/user可以得到如下返回值：

   {
     "errorCode": 0,
     "errorMessage": "",
     "data": {
       "name": "kotlin",
       "age": 12
     }
   }
   

   可以发现返回值也实现了文章开头需要的格式。
   这种方式的优势在于，Controller层无耦合，可以进行方便的重构。

总结

当需要对返回值进行统一的处理时，可以使用ResponseBodyAdvice来统一实现。免去了每一个Controller每一个接口都进行修改的问题。

思考

使用ResponseBodyAdvice虽然可以实现正常流程的返回值格式化。但是并没有实现党业务抛出异常时以及正常的业务出错时errorCode与errorMessage需要返回相应的错误代码。该如何实现呢？

现象

业务中用到了阿里云的ONS服务，开发中相同配置的情况下，在外网环境（mac开发机）上与阿里云ecs服务器上，服务启动时间相差巨大 （11.124 seconds与23.863 seconds的差距，相差接近10秒），查看日志并没有发现任何error出现，但是有一个奇怪的现象是，就是在外网环境启动时，两条日志记录的间隔时间也差不多是10秒左右。

解决思路

此时考虑，可能是main线程在这两条日志记录中间有耗时操作。于是打开VisualVM对java进程进行了thread dump。dump结果如下：

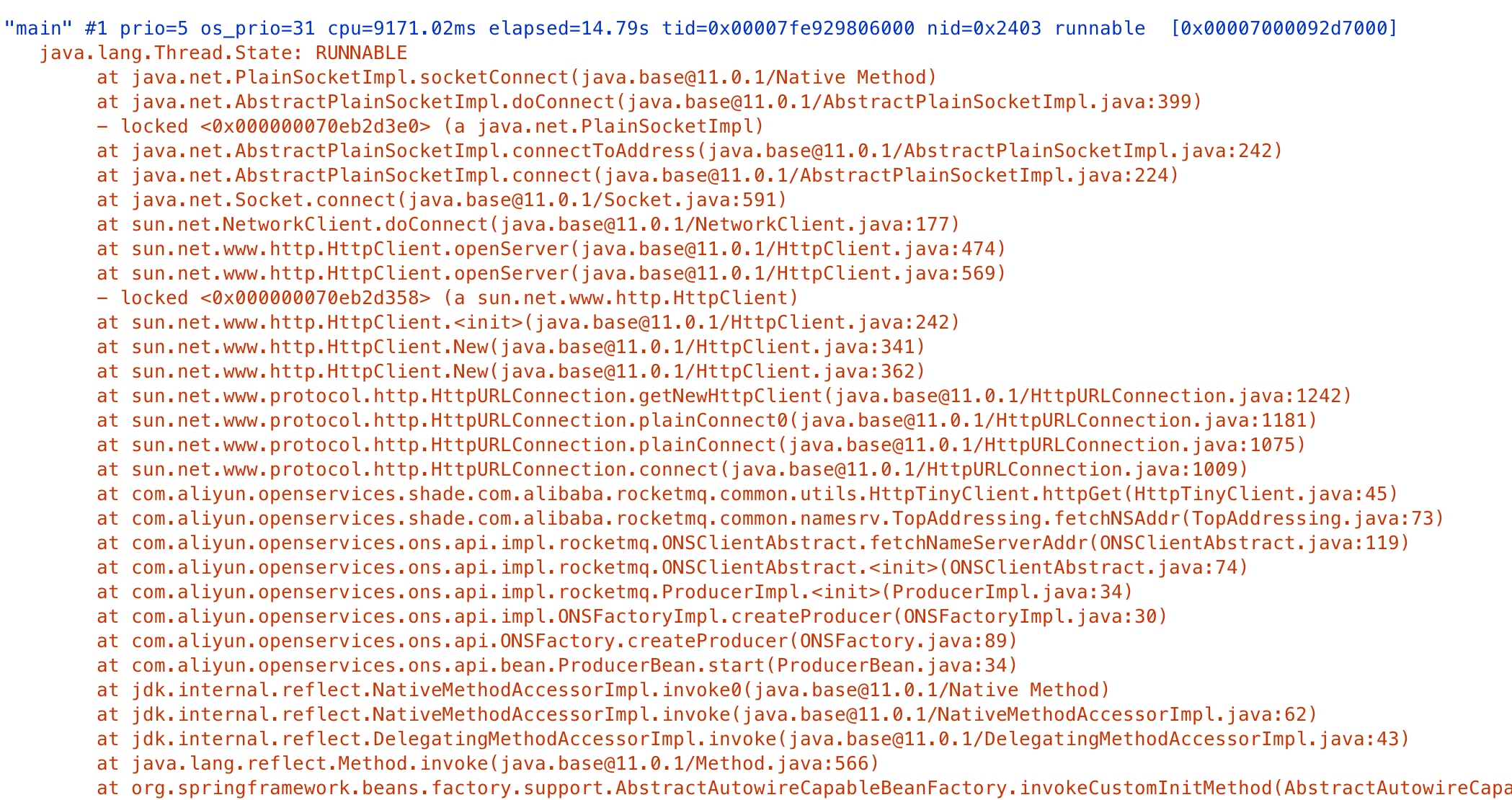
可以看到，调用栈在sun.net.www.http.HttpClient处锁住了，调用方是com.aliyun.openservices.shade.com.alibaba.rocketmq.common.utils.HttpTinyClient.httpGet 既然找到了位置，那么就可以加断点调试了。
加断点后调试查询发现，ons启动时会默认连接两个地址http://onsaddr-internet.aliyun.com/rocketmq/nsaddr4client-internet与http://onsaddr-internal.aliyun.com:8080/rocketmq/nsaddr4client-internal,前一个地址从url中可以看出就是个外网访问地址，但是后一个地址是一个内网地址。这样在外网环境下连接时会因为连接不上而超时，超时时间默认设置又是5秒，这也与项目中使用了两个队列相吻合。

解决方式

既然是默认连接两个地址，那么自然应该会有配置来设置只连内网或者只连外网。

private fun initProperties(): Properties {
    val properties = Properties()
    properties.setProperty(PropertyKeyConst.AccessKey, messageQueueProperties.accessKey)
    properties.setProperty(PropertyKeyConst.SecretKey, messageQueueProperties.secretKey)
    // 注意，一定要传这个值，否则外网启动会慢到死
    //properties.setProperty(PropertyKeyConst.ONSAddr, messageQueueProperties.onsAddr)
    return properties
}

这是我们配置ons的函数，可以看到默认是，是不设置PropertyKeyConst.ONSAddr这个配置的，这样ons启动时就会内网地址与外网地址同时连接。但是配置后，就只会连接设置的messageQueueProperties.onsAddr地址了。搭配spring的profile进行环境区分，不同环境配置不同的onsAddr就可以完美解决这个问题了。

实现方式

与Oracle的行锁不同，MySql的InnoDB行锁锁定的数据是对应的索引，而不是对应的行数据，也就是说，当检索条件不通过索引时，InnoDB将使用表锁进行锁定。实际应用中，如果不考虑这种情况，可能会造成大量的表锁冲突，影响并发性能。

示例

创建一个测试表并写入测试数据

create table innodb_lock (id int,name varchar(20));
insert into innodb_lock values(1,'a'),(2,'b'),(3,'c'),(4,'d');

注意：此时并没有创建索引。

mysql> select * from innodb_lock;
+------+------+
| id   | name |
+-------------+
|     1|a     |
|     2|b     |
|     3|c     |
|     4|d     |
+-------------+
4 rows in set (0.01 sec)

无索引情况

• 终端启动两个mysql客户端连入数据库

• 两个终端各自开启一个事务

   mysql> start transaction;
   Query OK, 0 rows affected (0.00 sec)
  

  为了方便起见，下文将两个事务分别命名为事务A与事务B

• 事务A 运行update命令修改id为4的数据的name列为e

  mysql> update innodb_lock set name='e' where id=4;
  Query OK, 1 row affected (0.07 sec)
  Rows matched: 1 Changed:1 Warnings:0
  mysql>
  

  注意此时事务A并没有提交事务。

• 事务B 同样运行update命令修改id为1的数据的name列为e

  mysql> update innodb_lock set name='e' where id=1;
  

  执行此命令后，客户端会卡在获取锁的阶段上。并没有直接返回。说明此时事务A已经锁住了整张表，与我们的预期一致。
  当事务B等待锁的时间超过innodb_lock_wait_timeout时，事务B会返回如下错误：

  mysql> update innodb_lock set name='e' where id=1;
  ERROR 1205 (HY000): Lock wait timeout exceeded; try restarting transaction
  

  innodb_lock_wait_timeout的默认设置为50秒。

• 事务A运行commit命令提交事务

  mysql> commit;
  Query OK, 0 rows affected (0.00 sec)
  

  此时观察事务B的返回会发现事务B的update操作也成功返回了。代表事务B获取到了表锁。
  事务B返回如下所示

  mysql> update innodb_lock set name='e' where id=1;
  Query OK, 1 row affected (4.08 sec)
  Rows matched: 1 Changed: 1 Warnings: 0
  

  从事务B的运行时间4.08sec也可以看出来事务B确实在获取锁时进行了等待

有索引的情况

• 相同的表结构与数据，但是增加了id为索引。

  mysql> alter table innodb_lock add index id_idx(id);
  Query OK, 0 rows affected (0.21 sec)
  Records: 0  Duplicates: 0  Warnings: 0
  

• 两个终端各自开启一个事务

  mysql> start transaction;
  Query OK, 0 rows affected (0.00 sec)
  

  为了方便起见，下文将两个事务分别命名为事务A与事务B

• 事务A 运行update命令修改id为4的数据的name列为e

  mysql> update innodb_lock set name='e' where id=4;
  Query OK, 0 rows affected (0.03 sec)
  Rows matched: 1  Changed: 0  Warnings: 0
  mysql>
  

  此时事务A同无索引情况一样并没有提交事务。

• 事务B 同样运行update命令修改id为1的数据的name列为e

  mysql> update innodb_lock set name='e' where id=1;
  Query OK, 0 rows affected (0.00 sec)
  Rows matched: 1  Changed: 0  Warnings: 0
  mysql>
  

可以发现，事务B并没有像无索引情况下那样阻塞住，而是马上返回了运行结果，说明此时事务A与B的锁粒度是行锁，而并不是表锁。同样可以说明MySql的行锁实现方式实际上是锁的索引而并不是行数据。

总结

MySql的行锁实现方式是对对应的索引进行锁定，而不是对对应的行进行锁定。如果命令并不是通过索引的方式进行锁定，那么锁将膨胀为表锁，此时在大并发量下会造成大量的锁等待，影响服务性能。

写在前面

关于BBR的原理可以参考知乎上的一个回答。

下载最新kernel

在http://kernel.ubuntu.com/~kernel-ppa/mainline/ 中下载最新的kernel。

这次我下载的是4.10的kernel，直接在终端中输入命令

wget http://kernel.ubuntu.com/\~kernel-ppa/mainline/v4.10/linux-image-4.10.0-041000-generic_4.10.0-041000.201702191831_amd64.deb

即可

安装kernel

运行命令

dpkg -i  linux-image-4.10.0-041000-generic_4.10.0-041000.201702191831_amd64.deb

后面的deb名称要根据你第一步下载的kernel而定。

（可选）删除其余kernel

查找内核

dpkg -l|grep linux-image 

删除上面列出的非此次安装的kernel

apt-get purge 旧内核

更新 grub 系统引导文件并重启

终端运行

update-grub
reboot

开启BBR

echo "net.core.default_qdisc=fq" >> /etc/sysctl.conf
echo "net.ipv4.tcp_congestion_control=bbr" >> /etc/sysctl.conf
sysctl -p

执行

sysctl net.ipv4.tcp_congestion_control

net.ipv4.tcp_congestion_control = bbr

lsmod | grep bbr

tcp_bbr                20480  78

最后

我的VPS使用的是StarryDNS的大阪机房。
北京联通直连不跳北美。想体验StarryDNS的可以通过这个链接来注册。