Copyright © 2015 Powered by MWeb, Theme used GitHub CSS.
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
说明:不允许修改给定的链表。
示例 1:
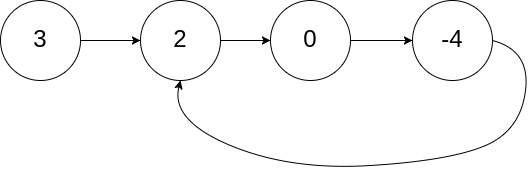
输入:head = [3,2,0,-4], pos = 1
输出:tail connects to node index 1
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
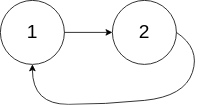
输入:head = [1,2], pos = 0
输出:tail connects to node index 0
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1
输出:no cycle
解释:链表中没有环。

进阶:
你是否可以不用额外空间解决此题?
我们在环形链表的问题中知道,可以使用快慢指针来判断一个链表是不是有环。但是该题目是需要返回链表的入环节点,仅使用快慢指针只是判断出了是否有环,所以还需要进一步的逻辑才能获取到入环节点。
假设链表有环,设入环点的为\(A\),从\(head\)到\(A\)的距离为\(a\),设快慢指针相交点为\(B\),从\(A\)到\(B\)的距离为\(b\),此时可得,慢指针走过的距离为\(a+b\),同时,我们知道快指针走过的距离是慢指针的一倍,即\(2*(a+b)\),此时可得如下结论,
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode detectCycle(ListNode head) {
if (head == null || head.next == null) {
return null;
}
//使用快慢指针的方式进行
ListNode fast = head;
ListNode slow = head;
while (fast != null && fast.next != null && fast.next.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) {
//此时说明有环,需要处理
fast = head;
while(true) {
if (slow == fast) {
return slow;
}
slow = slow.next;
fast = fast.next;
}
}
}
//无环状态
return null;
}
}
给定一个链表和一个特定值 \(x\),对链表进行分隔,使得所有小于 \(x \)的节点都在大于或等于\(x\)的节点之前。
你应当保留两个分区中每个节点的初始相对位置。
示例:
输入: \(head = 1->4->3->2->5->2, x = 3\)
输出: \(1->2->2->4->3->5\)
新建两个\(dummyHead\),其中一个保存所有小于\(x\)的节点,另一个保存所有大于等于\(x\)的节点。最后拼接两个链表就行了。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode partition(ListNode head, int x) {
ListNode dummy1 = new ListNode(1);
ListNode dummy2 = new ListNode(1);
ListNode node1 = dummy1;
ListNode node2 = dummy2;
while(head != null) {
if (head.val < x) {
node1.next = head;
head = head.next;
node1 = node1.next;
node1.next = null;
} else {
node2.next = head;
head = head.next;
node2 = node2.next;
node2.next = null;
}
}
node1.next = dummy2.next;
return dummy1.next;
}
}
整体也没什么难度。需要注意的就是在
给定两个有序整数数组 nums1 和 nums2,将 nums2 合并到 nums1 中,使得 num1 成为一个有序数组。
说明:
示例:
输入:
\(nums1 = [1,2,3,0,0,0], m = 3\)
\(nums2 = [2,5,6], n = 3\)
输出: \([1,2,2,3,5,6]\)
如果正序对比,那么会涉及到\(nums1\)数组的元素右移,时间复杂度非常高。直接排除掉这种做法。
考虑倒序对比,会发现这样一种情况,最终合并到\(nums1\)数组中的数据,最大值的位置是在\(m+n-1\)处,而通过观察可以发现,\(m+n-1\)是必然大于等于\(m-1\)的。这样在倒序合并时,并不会覆盖掉\(nums1\)的原始数值的。这里的循环跳出条件是,\(nums1\)已经扫描完了,或者\(nums2\)已经扫描完了。但是需要注意的一点是,跳出后,如果是\(nums2\)扫描完了,那么可以直接返回;如果是\(nums1\)扫描完了,仍然需要把\(nums2\)的数据写回到\(nums1\)中去。
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int i=m+n-1;
while(m>0 && n>0) {
if(nums1[m-1] >= nums2[n-1]){
nums1[i--] = nums1[m-1];
m--;
} else {
nums1[i--] = nums2[n-1];
n--;
}
}
while(n>0) {
nums1[i--] = nums2[n-1];
n--;
}
}
}
代码整体没有难度。注意哪个指针往前移就可以了。
给定一个链表,删除链表的倒数第 \(n\) 个节点,并且返回链表的头结点。
示例:
给定一个链表: 1->2->3->4->5, 和 n = 2.
当删除了倒数第二个节点后,链表变为 1->2->3->5.
说明:
给定的 \(n\) 保证是有效的。
进阶:
你能尝试使用一趟扫描实现吗?
使用双指针来处理。\(fast\)指针先走\(n\)步,然后\(fast\)指针与\(slow\)指针同时推进,当\(fast\)指针走到链表尾时,\(slow\)指针正好走到倒数\(n+1\)的位置。这时候只需要\(slow.next = slow.next.next\)即可,但是如果直接使用\(head\)作为开头有很多的不便。比如\(n\)等于链表长度,此时,要删除的其实为\(head\)节点,但是此时很难去判断究竟是要删除\(slow\)节点,还是\(slow.next\)节点。
为了排除这种情况,我们引入一个\(dummy\)节点,\(dummy.next = head\),在删除时永远只删除\(slow.next\),这样我们无论怎么处理链表,最终链表的\(head\)均为\(dummy.next\)。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0);
dummy.next = head;
ListNode fast = dummy;
ListNode slow = dummy;
//fast节点先走n步,此处不需要考虑fast.next是否为null,题目保证了n是个有效的数字。
for(int i = 1; i <= n; i++) {
fast = fast.next;
}
//开始同时推进fast与slow,这里循环跳出条件是fast.next ==null,即fast已经到了end。
while (fast.next != null) {
fast = fast.next;
slow = slow.next;
}
//此时slow已经到了倒数n+1的位置。但是仍然需要判断slow.next是否为null,防止NPE
if (slow.next != null) {
slow.next = slow.next.next;
}
//dummy.next为head。返回即可
return dummy.next;
}
}
给定一个包含红色、白色和蓝色,一共 \(n\) 个元素的数组,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
此题中,我们使用整数 \(0、 1 和 2 \)分别表示红色、白色和蓝色。
注意:
不能使用代码库中的排序函数来解决这道题。
示例:
输入: \([2,0,2,1,1,0]\)
输出: \([0,0,1,1,2,2]\)
进阶:
一个直观的解决方案是使用计数排序的两趟扫描算法。
- 首先,迭代计算出0、1 和 2 元素的个数,然后按照0、1、2的排序,重写当前数组。
- 你能想出一个仅使用常数空间的一趟扫描算法吗?
进阶中给出了一种解决方案。两次循环就可以完成。
class Solution {
public void sortColors(int[] nums) {
if (nums==null || nums.length<2) {
return;
}
//数组中0的数量
int i=0;
//数组中1的数量
int j=0;
//数组中2的数量不需要计算,因为当i与j都是0时,剩下的肯定都是2
//开始第一次循环,获取i与j
for(int n:nums) {
if (n==0) {
i++;
} else if (n==1) {
j++;
}
}
//开始第二次循环,将0,1,2重新写入数组
for(int l = 0;l<nums.length;l++) {
if (i>0) {
nums[l]=0;
} else if (j>0) {
nums[l] = 1;
} else {
nums[l] = 2;
}
}
}
}
这其实就是荷兰国旗算法。算法如下:
整体算法比较直观,需要注意的一点是,当前值为\(2\)时,\(curr\)并不往前推进,而是停留在原地。这个的原因在于,如果\(nums_{end}=0\),在本次交换后,\(nums_{curr}=0\),下一轮需要将\(0\)交换给\(begin\)。因此,这种情况下\(curr\)不能往前推进。
还有一个需要注意的地方在于,就是循环的终止条件,如果没有思考清楚,那么很有可能就写成了\(curr<end\),但是这种情况是错的。考虑这样一个输入数组\([2,0,1]\),在第一轮的判断时,是走的如上第三种情况,这样\(end\)在第二轮时就是1了,如果是\(curr<end\)的判断的话,那么这一步就跳出循环了。最终结果就是\([1,0,2]\),第二个元素并没有参与到比较中来。所以循环的规则应该是\(curr<=end\)。
class Solution {
public void sortColors(int[] nums) {
if (nums == null || nums.length < 2) {
return;
}
//三个指针的初始化,
int begin = 0, curr = 0, end = nums.length-1;
//循环的判断条件见解法中的说明
while (curr <= end){
//第一种情况
if (nums[curr] == 0) {
nums[curr] = nums[begin];
nums[begin] = 0;
curr++;
begin++;
} else if (nums[curr] == 1) {
//第二种情况
curr++;
} else {
nums[curr] = nums[end];
nums[end] = 2;
end--;
}
}
}
给定一个链表,旋转链表,将链表每个节点向右移动 \(k\) 个位置,其中 \(k\)是非负数。
示例 1:
输入: \(1->2->3->4->5->NULL, k = 2\)
输出: \(4->5->1->2->3->NULL\)
解释:
向右旋转 1 步: \(5->1->2->3->4->NULL\)
向右旋转 2 步: \(4->5->1->2->3->NULL\)
示例 2:
输入: \(0->1->2->NULL, k = 4\)
输出: \( 2->0->1->NULL\)
解释:
向右旋转 1 步: \(2->0->1->NULL\)
向右旋转 2 步: \(1->2->0->NULL\)
向右旋转 3 步: \(0->1->2->NULL\)
向右旋转 4 步: \(2->0->1->NULL\)
一开始可以发现,有如下三种特殊情况是可以直接不进行任何处理,直接返回head的:
考虑\(k\)的取值, 如果\(k\)的值正好是链表长度的整数倍,这种情况右移后还是原链表本身。返回即可。
接下来,如果\(k\)远远超过链表的长度,我们也没必要进行过多的右移,获取\(k\)对链表长度的余数即为右移的次数。
一个难点在于,在单向链表中找到一个元素的父亲节点的时间复杂度很高。此时第一个想法是翻转链表、新链表左移、再次翻转链表。
也写出了第一版代码。
class Solution {
public ListNode rotateRight(ListNode head, int k) {
//三种情况,链表为空、链表只有一个元素、移动位置为0
if (head == null ||head.next == null || k == 0) {
return head;
}
ListNode tail = head;
ListNode temp = head;
//判断长度
int i = 1;
while (temp.next != null) {
temp = temp.next;
i++;
}
k = k % i;
//当旋转整数倍时,没有必要挪动数据,直接返回head
if (k == 0) {
return head;
}
//翻转链表
head = reverse(head);
while(k>0) {
tail.next = head;
tail = head;
head = head.next;
tail.next = null;
k--;
}
head = reverse(head);
return head;
}
//翻转链表
ListNode reverse (ListNode head) {
ListNode prev = head;
ListNode curr = head.next;
while (curr!=null) {
ListNode temp = curr.next;
curr.next = prev;
prev = curr;
curr = temp;
}
head.next = null;
return prev;
}
}
解法1的问题在于有两次翻转链表,虽然只是\(O(n)\)的时间复杂度,但是本着能少一步是一步的原则,还是能省则省。
继续观察示例1,发现,右移\(2\)位,实际上是左移\(3\)位,而左移是解法1里就实现了的。这就不需要翻转链表就可以直接移动了。
class Solution {
public ListNode rotateRight(ListNode head, int k) {
//三种情况,链表为空、链表只有一个元素、移动位置为0
if (head == null ||head.next == null || k == 0) {
return head;
}
ListNode tail = head;
ListNode temp = head;
//判断长度
int i = 1;
while (tail.next != null) {
temp = tail;
tail = tail.next;
i++;
}
k = k % i;
//当旋转整数倍时,没有必要挪动数据,直接返回head
if (k == 0) {
return head;
}
//增加了一步k的计算
k = i-k;
//翻转链表
//注释掉解法1的翻转链表
//head = reverse(head);
while(k>0) {
tail.next = head;
tail = head;
head = head.next;
tail.next = null;
k--;
}
//注释掉解法1的翻转链表
//head = reverse(head);
return head;
}
//翻转链表
ListNode reverse (ListNode head) {
ListNode prev = head;
ListNode curr = head.next;
while (curr!=null) {
ListNode temp = curr.next;
curr.next = prev;
prev = curr;
curr = temp;
}
head.next = null;
return prev;
}
}
仔细观察代码,实际上是去掉了翻转链表,对k进行了更进一步的操作而已。相比解法一,代码更加的清晰。
给定一个数组\( nums\) 和一个值 \(val\),你需要原地移除所有数值等于 \(val\) 的元素,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在原地修改输入数组并在使用 \(O(1)\) 额外空间的条件下完成。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1:
给定 \(nums = [3,2,2,3], val = 3\),
函数应该返回新的长度 \(2\), 并且 \(nums\) 中的前两个元素均为 \(2\)。
你不需要考虑数组中超出新长度后面的元素。
示例 2:
给定 \(nums = [0,1,2,2,3,0,4,2], val = 2\),
函数应该返回新的长度 \(5\), 并且 \(nums\) 中的前五个元素为 \(0, 1, 3, 0, 4\)。
注意这五个元素可为任意顺序。
你不需要考虑数组中超出新长度后面的元素。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以“引用”方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:// nums 是以“引用”方式传递的。也就是说,不对实参作任何拷贝 int len = removeElement(nums, val); // 在函数里修改输入数组对于调用者是可见的。 // 根据你的函数返回的长度, 它会打印出数组中该长度范围内的所有元素。 for (int i = 0; i < len; i++) { print(nums[i]); }
使用双指针,从数组的两头分别扫描,左指针停在等于\(val\)的位置,右指针停在不等于\(val\),然后交换两个指针的值,进行下一轮扫描。
class Solution {
public int removeElement(int[] nums, int val) {
int left = 0;
int right = nums.length - 1;
while (left < right) {
//左指针停在等于val的位置
while (left < nums.length && nums[left] != val) {left++;}
//右指针停在不等val的位置
while (right > 0 && num[right] == val) {right--;}
//判断两个指针的位置是不是正确,正确的话就交换,否则说明已经超过位置了,直接跳出即可
if (left<right) {
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
} else {
break;
}
}
return left;
}
}
给定一个排序数组,你需要在原地删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在原地修改输入数组并在使用 \(O(1)\) 额外空间的条件下完成。
示例 1:
给定数组\( nums = [1,1,2]\),
函数应该返回新的长度 \(2\), 并且原数组 \(nums\) 的前两个元素被修改为 \(1, 2\)。
你不需要考虑数组中超出新长度后面的元素。
示例 2:
给定 \(nums = [0,0,1,1,1,2,2,3,3,4]\),
函数应该返回新的长度 \(5\), 并且原数组 \(nums\) 的前五个元素被修改为 \(0, 1, 2, 3, 4\)。
你不需要考虑数组中超出新长度后面的元素。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以“引用”方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参做任何拷贝int len = removeDuplicates(nums); // 在函数里修改输入数组对于调用者是可见的。 // 根据你的函数返回的长度, 它会打印出数组中该长度范围内的所有元素。 for (int i = 0; i < len; i++) { print(nums[i]); }
快慢指针,慢指针只有在快指针的数大于慢指针前一个数时才推进。
class Solution {
public int removeDuplicates(int[] nums) {
int index=0;
for(int n:nums) {
if(index<1||n>nums[index-1]) {
nums[index++]=n;
}
}
return index;
}
}
给定一个排序数组,你需要在原地删除重复出现的元素,使得每个元素最多出现两次,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在原地修改输入数组并在使用 \(O(1)\) 额外空间的条件下完成。
示例 1:
给定 \(nums = [1,1,1,2,2,3]\),
函数应返回新长度 \(length = 5\), 并且原数组的前五个元素被修改为 \(1, 1, 2, 2, 3\) 。
你不需要考虑数组中超出新长度后面的元素。
示例 2:
给定 \(nums = [0,0,1,1,1,1,2,3,3]\),
函数应返回新长度 \(length = 7\), 并且原数组的前五个元素被修改为 \(0, 0, 1, 1, 2, 3, 3\) 。
你不需要考虑数组中超出新长度后面的元素。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以“引用”方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参做任何拷贝 int len = removeDuplicates(nums);
// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中该长度范围内的所有元素。
for (int i = 0; i < len; i++) {
print(nums[i]);
}
使用快慢指针,快指针每次循环都往前推进,慢指针只有在指针位置小于2(前面两位必然需要向前推进)或者慢指针前推2位的数小于快指针的数时,才向前推进,并且将快指针的值赋值到慢指针位置。
class Solution {
public int removeDuplicates(int[] nums) {
int fast=0;
int slow=0;
while(fast<nums.length) {
//慢指针只有在小于2或者前数2位小于快指针时才往前推进
if (slow < 2 || nums[fast] > nums[slow-2]) {
nums[slow] = nums[fast];
slow++;
}
fast++;
}
return slow;
}
}
给定一个包含 \(n + 1\) 个整数的数组 \(nums\),其数字都在 \(1\) 到 \(n\) 之间(包括 \(1\) 和 \(n\)),可知至少存在一个重复的整数。假设只有一个重复的整数,找出这个重复的数。
示例 1:
输入: \([1,3,4,2,2]\)
输出: \(2\)
示例 2:
输入: \([3,1,3,4,2]\)
输出: \(3\)
说明:
不能更改原数组(假设数组是只读的)。
只能使用额外的 \(O(1)\) 的空间。
时间复杂度小于 \(O(n^2)\) 。
数组中只有一个重复的数字,但它可能不止重复出现一次。
查看题目,其数字均在\(1\) 到 \(n\) 之间,因此,可以将数字当作数组下标,指向下一个数组元素,那么就可以把数组\(nums\)当成一个链表,题目就成为了将查询链表的环的入口。
链表判断环可以使用快慢指针。
class Solution {
public int findDuplicate(int[] nums) {
int fast = 0;
int slow = 0;
while (true) {
fast = nums[nums[fast]];
slow = nums[slow];
if (fast == slow) {
fast = 0;
while(fast != slow) {
fast = nums[fast];
slow = nums[slow];
}
return nums[slow];
}
}
}
}
Copyright © 2015 Powered by MWeb, Theme used GitHub CSS.