Copyright © 2015 Powered by MWeb, Theme used GitHub CSS.
给定一个二叉树,找到最长的路径,这个路径中的每个节点具有相同值。 这条路径可以经过也可以不经过根节点。
**注意:**两个节点之间的路径长度由它们之间的边数表示。
示例 1:
输入:
5
/ \
4 5
/ \ \
1 1 5
输出 \(2\)
示例 2:
输入:
1
/ \
4 5
/ \ \
4 4 5
输出: \(2\)
注意: 给定的二叉树不超过\(10000\)个结点。 树的高度不超过\(1000\)。
基本想法就是深度优先遍历。遍历时,判断左右儿子的值与自己的值是否相等,相等则result++,否则置为0即可。没有什么难度。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private int result = 0;
public int longestUnivaluePath(TreeNode root) {
if (root != null) {
dfs(root);
}
return result;
}
private int dfs(TreeNode root) {
if (root ==null) {
return 0;
}
//计算左子树的同值路径
int left = dfs(root.left);
//判断左儿子与自己的值是否相等,相等则++ 否则置为0
if (root.left == null || root.val !=root.left.val) {
left = 0;
} else {
left ++;
}
//计算右子树的同值路径
int right = dfs(root.right);
//同左儿子的判断
if (root.right == null || root.val !=root.right.val) {
right = 0;
} else {
right ++;
}
//需要注意的是这里的max为left+right与result的判断。
result = Math.max(left + right,result);
return Math.max(left, right);
}
}
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过根结点。
示例 :
给定二叉树
digraph G {
{
node [margin=0 width=0.1 shape=circle style=filled]
1 -> 2 [arrowhead=none]
1 -> 3 [arrowhead=none]
2 -> 4 [arrowhead=none]
2 -> 5 [arrowhead=none]
}
}
返回\(3\),它的长度是路径 \([4,2,1,3]\) 或者 \([5,2,1,3]\)。
**注意:**两结点之间的路径长度是以它们之间边的数目表示。
此题是二叉树深度搜索的扩展,考虑设置一个全局变量result,每次递归时判断一次左子树深度+右子树深度 是否大于result,如果大于,那么将result替换成和,递归完成时,返回result即可。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private int result = 0;
public int diameterOfBinaryTree(TreeNode root) {
// 深度优先遍历+判断一次result大小即可。
dfs(root);
return result;
}
private int dfs(TreeNode root) {
if (root == null) {
return 0;
}
//递归左子树
int right = dfs(root.right);
//递归右子树
int left = dfs(root.left);
//左子树深度+右子树深度就是走过当前节点的直径长度
if (left + right > result) {
result = left + right;
}
//返回当前节点深度+1.递归到上一层参与计算
return Math.max(left, right) + 1;
}
}
给定一个正整数数组 \(nums\)。
找出该数组内乘积小于 \(k\) 的连续的子数组的个数。
示例 1:
输入: \(nums = [10,5,2,6], k = 100\)
输出: \(8\)
解释: \(8\)个乘积小于\(100\)的子数组分别为: \([10], [5], [2], [6], [10,5], [5,2], [2,6], [5,2,6]\)。
需要注意的是 \([10,5,2]\) 并不是乘积小于100的子数组。
说明:
第一想法是使用双指针一直乘,当结果小于\(k\)时,将\(fast\)指针与\(slow\)指针之间的子数组数量加到结果\(result\)中。但是难点在于如何排重。
我们会注意到这样一种规律:
此时会发现,\(fast\)与\(fast-1\)子数组的区别仅在于是否包含\(nums[fast]\)元素,而包含全部\(nums[fast]\)元素的子数组数量为\(fast-slow+1\),这个值,就排除了重复的子数组,\(result\)对这个数字进行暂存就可以在循环结束后直接得到数组数量。
可能说的有些乱,下面给出一个例子,\([1,2,3]\)数组,当\(slow=0,fast=2\)时,此时,全部的子数组为\([1],[2],[1,2]\),当\(slow=0,fast=3\)时,此时的子数组为\([1],[2],[1,2],[1,2,3],[2,3],[3]\),对比两个子数组可以发现,两者的区别就在于多了包含\(fast\)的元素的数组。
当乘积不满足条件时,乘积除以\(slow\)指针元素,\(slow\)指针前进,
class Solution {
public int numSubarrayProductLessThanK(int[] nums, int k) {
// slow为慢指针,mul为slow与fast之间的乘积,result为满足条件的数组个数.
int slow = 0, mul = 1, result = 0;
for (int fast = 0; fast < nums.length; fast++) {
// fast指针前移,mul计算新的乘积。
mul *= nums[fast];
//此时判断mul是否已经大于k了,当大于时,需要除slow元素直到满足条件为止
while (mul >= k && slow <= fast) {
mul /= nums[slow++];
}
//这里可能会有疑问需不需要判断slow与fast的大小,其实这里不需要判断,前一步如果slow超过fast了,下一轮时,fast会赶上来。而且slow最多比fast多1,两者相减再加一等于0,符合数组数量为0,不用担心减成负数
result += fast - slow + 1;
}
return result;
}
}
给定一个含有 \(n\) 个正整数的数组和一个正整数 \(s \),找出该数组中满足其和 \(≥ s \)的长度最小的连续子数组。如果不存在符合条件的连续子数组,返回\( 0\)。
示例:
输入: \(s = 7, nums = [2,3,1,2,4,3]\)
输出: \(2\)
解释: 子数组 \([4,3]\) 是该条件下的长度最小的连续子数组。
进阶:
如果你已经完成了\(O(n)\) 时间复杂度的解法, 请尝试\( O(n log n)\) 时间复杂度的解法。
连续子数组,考虑使用双指针\(start\)与\(end\)滑动窗口来判断.设置一个\(sum\)值,表示滑动窗口中的和,每一轮循环,判断\(sum\)与\(s\)的关系,有两种情况:
class Solution {
public int minSubArrayLen(int s, int[] nums) {
// 注意这里的end的起始位置
int start = 0, end = -1;
int result = Integer.MAX_VALUE, sum = 0;
// 开始循环,循环跳出的条件是start指针循环到数组尾部了
while (start < nums.length) {
// 这里需要注意判断条件
if (sum < s && end + < nums.length) {
end++;
sum += nums[end];
} else {
sum -= nums[start];
start++;
}
if (sum >= s) result = result < end - start + 1 ? result : end - start + 1;
}
return result == Integer.MAX_VALUE ? 0 : result;
}
}
给定两个字符串 \(s1 \)和 \(s2\),写一个函数来判断 \(s2\) 是否包含 \(s1\) 的排列。
换句话说,第一个字符串的排列之一是第二个字符串的子串。
示例1:
输入: \(s1 = "ab" s2 = "eidbaooo"\)
输出: \(True\)
解释: \(s2\) 包含 \(s1\) 的排列之一 \(("ba")\).
示例2:
输入: \(s1= "ab" s2 = "eidboaoo"\)
输出: \(False\)
注意:
题目乍一看似乎没什么好办法,暴力遍历总是行得通。但是时间复杂度嘛,嘿嘿。
接下来深挖一下题目,既然是判断\(s2\)是否包含\(s1\),那么我们总是可以排除一些明显不满足条件的地方:
接下来,我们假设\(s2\)中有\(s1\)的排列\(a\),那么这个排列\(a\)的长度肯定是\(s1\)的长度\(length\),实际上就是判断这两个字符串不管字母顺序是否相同,
判断两个字符串是否相同可以用一个长度为26的数组,遍历第一个,将字母出现的次数记下来,然后遍历另一个字符串将数组中字母出现的次数减小一,当次数减小到-1时,代表不相同,直接返回false。当遍历完仍然没有返回时,那么两个字符串肯定是相同的。
我们可以设置两个指针,一个起始指针\(start\),一个结束指针\(end\),并且有\(end = start +length - 1\)。此时,从\(end\)指针处往回判断。至于为什么从\(end\)处往回走而不是从\(start\)处往前走是因为,我们注意到这样一种情况,当\(end\)处的字符在数组中出现次数已经减到0时,\(end\)处的字符必然不在排列\(a\)中,此时,\(start\)可以直接跳到\(end+1\)处,可以直接过滤掉部分字符。这样也就不用遍历必然失败的场景了。
class Solution {
public boolean checkInclusion(String s1, String s2) {
// 特殊情况直接跳出
if (s1 == null || s2 == null || s2.length() < s1.length()) {
return false;
}
// 初始化一个数组,将s1的字母出现次数保存在这个数组中去。
int[] map = new int[26];
int length = s1.length();
//遍历s1放入map
for (int i = 0; i < length; i++) {
map[s1.charAt(i) - 'a']++;
}
//遍历s2,此时注意到这样一个情况,如果s2包含s1,那么s2子串的长度必然等于s1,因此,可以设置两个指针。
int start = 0, end = length - 1;
while (end < s2.length()) {
// 这里是一个注意点,需要注意不能直接用map处理,否则会导致第一次false后,后面的判断全是false
int[] temp = map.clone();
while (end >= start) {
if (temp[s2.charAt(end) - 'a']-- == 0) {
break;
}
end--;
}
//上一层有两种跳出方式,一种break;一种是正确判断完了。需要区分一下。
if (end < start) {
//这种是正常判断完成了。直接返回true
return true;
} else {
//此时注意到这样一种情况,end处必然不能在s2子串中出现。那么start = end+1,end = start+length-1 可以跳过start与end之间的字符,因为这部分字符必然不满足条件。
start = end + 1;
end = start + length - 1;
}
}
return false;
}
}
编写一个函数,其作用是将输入的字符串反转过来。
示例 1:
输入: "hello"
输出: "olleh"
示例 2:
输入: "A man, a plan, a canal: Panama"
输出: "amanaP :lanac a ,nalp a ,nam A"
使用双指针分别从字符串开始位置转到字符串结束位置就可以了。整体没有难度。
class Solution {
public String reverseString(String s) {
char[] chars = s.toCharArray();
int start= 0, end = chars.length - 1;
while (start < end) {
char temp = chars[start];
chars[start++] = chars[end];
chars[end--] = temp;
}
return String.valueOf(chars);
}
}
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
说明:不允许修改给定的链表。
示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:tail connects to node index 1
解释:链表中有一个环,其尾部连接到第二个节点。
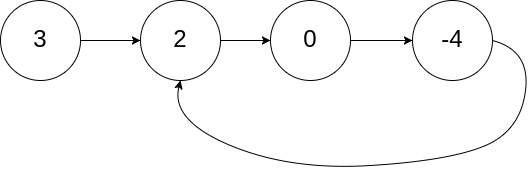
示例 2:
输入:head = [1,2], pos = 0
输出:tail connects to node index 0
解释:链表中有一个环,其尾部连接到第一个节点。
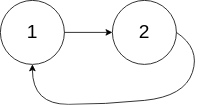
示例 3:
输入:head = [1], pos = -1
输出:no cycle
解释:链表中没有环。

进阶:
你是否可以不用额外空间解决此题?
我们在环形链表的问题中知道,可以使用快慢指针来判断一个链表是不是有环。但是该题目是需要返回链表的入环节点,仅使用快慢指针只是判断出了是否有环,所以还需要进一步的逻辑才能获取到入环节点。
假设链表有环,设入环点的为\(A\),从\(head\)到\(A\)的距离为\(a\),设快慢指针相交点为\(B\),从\(A\)到\(B\)的距离为\(b\),此时可得,慢指针走过的距离为\(a+b\),同时,我们知道快指针走过的距离是慢指针的一倍,即\(2*(a+b)\),此时可得如下结论,
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode detectCycle(ListNode head) {
if (head == null || head.next == null) {
return null;
}
//使用快慢指针的方式进行
ListNode fast = head;
ListNode slow = head;
while (fast != null && fast.next != null && fast.next.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) {
//此时说明有环,需要处理
fast = head;
while(true) {
if (slow == fast) {
return slow;
}
slow = slow.next;
fast = fast.next;
}
}
}
//无环状态
return null;
}
}
给定一个链表和一个特定值 \(x\),对链表进行分隔,使得所有小于 \(x \)的节点都在大于或等于\(x\)的节点之前。
你应当保留两个分区中每个节点的初始相对位置。
示例:
输入: \(head = 1->4->3->2->5->2, x = 3\)
输出: \(1->2->2->4->3->5\)
新建两个\(dummyHead\),其中一个保存所有小于\(x\)的节点,另一个保存所有大于等于\(x\)的节点。最后拼接两个链表就行了。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode partition(ListNode head, int x) {
ListNode dummy1 = new ListNode(1);
ListNode dummy2 = new ListNode(1);
ListNode node1 = dummy1;
ListNode node2 = dummy2;
while(head != null) {
if (head.val < x) {
node1.next = head;
head = head.next;
node1 = node1.next;
node1.next = null;
} else {
node2.next = head;
head = head.next;
node2 = node2.next;
node2.next = null;
}
}
node1.next = dummy2.next;
return dummy1.next;
}
}
整体也没什么难度。需要注意的就是在
给定两个有序整数数组 nums1 和 nums2,将 nums2 合并到 nums1 中,使得 num1 成为一个有序数组。
说明:
示例:
输入:
\(nums1 = [1,2,3,0,0,0], m = 3\)
\(nums2 = [2,5,6], n = 3\)
输出: \([1,2,2,3,5,6]\)
如果正序对比,那么会涉及到\(nums1\)数组的元素右移,时间复杂度非常高。直接排除掉这种做法。
考虑倒序对比,会发现这样一种情况,最终合并到\(nums1\)数组中的数据,最大值的位置是在\(m+n-1\)处,而通过观察可以发现,\(m+n-1\)是必然大于等于\(m-1\)的。这样在倒序合并时,并不会覆盖掉\(nums1\)的原始数值的。这里的循环跳出条件是,\(nums1\)已经扫描完了,或者\(nums2\)已经扫描完了。但是需要注意的一点是,跳出后,如果是\(nums2\)扫描完了,那么可以直接返回;如果是\(nums1\)扫描完了,仍然需要把\(nums2\)的数据写回到\(nums1\)中去。
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int i=m+n-1;
while(m>0 && n>0) {
if(nums1[m-1] >= nums2[n-1]){
nums1[i--] = nums1[m-1];
m--;
} else {
nums1[i--] = nums2[n-1];
n--;
}
}
while(n>0) {
nums1[i--] = nums2[n-1];
n--;
}
}
}
代码整体没有难度。注意哪个指针往前移就可以了。
给定一个链表,删除链表的倒数第 \(n\) 个节点,并且返回链表的头结点。
示例:
给定一个链表: 1->2->3->4->5, 和 n = 2.
当删除了倒数第二个节点后,链表变为 1->2->3->5.
说明:
给定的 \(n\) 保证是有效的。
进阶:
你能尝试使用一趟扫描实现吗?
使用双指针来处理。\(fast\)指针先走\(n\)步,然后\(fast\)指针与\(slow\)指针同时推进,当\(fast\)指针走到链表尾时,\(slow\)指针正好走到倒数\(n+1\)的位置。这时候只需要\(slow.next = slow.next.next\)即可,但是如果直接使用\(head\)作为开头有很多的不便。比如\(n\)等于链表长度,此时,要删除的其实为\(head\)节点,但是此时很难去判断究竟是要删除\(slow\)节点,还是\(slow.next\)节点。
为了排除这种情况,我们引入一个\(dummy\)节点,\(dummy.next = head\),在删除时永远只删除\(slow.next\),这样我们无论怎么处理链表,最终链表的\(head\)均为\(dummy.next\)。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0);
dummy.next = head;
ListNode fast = dummy;
ListNode slow = dummy;
//fast节点先走n步,此处不需要考虑fast.next是否为null,题目保证了n是个有效的数字。
for(int i = 1; i <= n; i++) {
fast = fast.next;
}
//开始同时推进fast与slow,这里循环跳出条件是fast.next ==null,即fast已经到了end。
while (fast.next != null) {
fast = fast.next;
slow = slow.next;
}
//此时slow已经到了倒数n+1的位置。但是仍然需要判断slow.next是否为null,防止NPE
if (slow.next != null) {
slow.next = slow.next.next;
}
//dummy.next为head。返回即可
return dummy.next;
}
}
Copyright © 2015 Powered by MWeb, Theme used GitHub CSS.